Products  Main  Summary  FAQ  Customers  Contact  TOC  Choose format

FAQ - Mathematics of UPE

1. Can you describe UPE intuitively?
2. What do you claim precisely?
3. How secure key hiding works?
4. What are the closest mathematical results to UPE?
5. Are there other applications of UPE than security?

Can you describe UPE intuitively?

This section is an informal description of the universal program encryption (UPE) protocol, invented by Tibor Ódor. All rights belong to Tamper-Proof Verified Systems (TPVS), Hungary. For a more formal description see the next section. For its most simple and important application the secure key hiding technology see the third section.

The general idea is as follows. We transform the program P into an other one Q. The program Q looses the original structure of  P and it is totally incomprehensible, nevertheless it computes the same function as P does in more or less the same time and space as P. All of its particular features occur "everywhere", one cannot localize them.  We make a kind of hologram from the original program. The program and its execution looks totally random.

To put it even more simply, from one executable we make an equivalent one with no clues left, so that no one can figure out what and how it does this. Nevertheless, the "what it does" part of the problem can be solved for simple programs - but not feasibly proved.

UPE is an active form of encryption, unlike text encryption, which is passive. It poses unique dangers which make special constraints on our strategy.

The theoretical and practical consequences of this statement are enormous. It completely reshapes the vision about and understanding of computer, data and digital content security and integrity.  It has the potential to redefine and redistribute power, property and control in cyberspace.

For a more formal description see the next section. For the most simple and important application of UPE see the third section.

Back to Top

What do you claim precisely?

This section is the precise description of the universal program encryption (UPE) protocol, invented by Tibor Ódor. All rights belong to Tamper-Proof Verified Systems (TPVS), Hungary. For a less formal description see the previous section. For its most simple and important application the secure key hiding technology see the third section.

In the abstract one work tape, one read-only input and write-only output tape Turing machine model we claim that there is an universal Turing machine that for any program P we can provide a program Q with the following properties. 

• Let m be a so called security constant. The length q of the program Q is 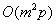, where p is the length of the program P.

• The running space is O(f(x)) for any function f(x) > s(x), where s(x) is the running space of P for the input x, and f(x) is computable in space O(f(x)) and time h(x) and the length of program which computes f is less than O(p).

• If the running time for a particular input x is t(x) then Q runs on 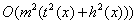. It writes the output to the output tape exactly at the end.

• One cannot distinguish the program Q, the movement of the head of the Turing machine, its read and write operations and the content of its work tape from randomness, unless P=NP.

• To crack Q (that is to find a program R with a simple two way equivalence to P) is NP complete. One need at least exp(O(m)) time with all recently known algorithms to crack it.

• The program Q is computed in polynomial (in the length of P) time from P. For more special class of programs or other computational models far better performance is possible. (For example, Q may run in linear, i.e. in 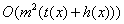time.)

It may change the validity of the above statements if additional information is known about the program P or about its structure. If this occurs, some further special care is necessary. (This is not unlike the encryption of yes/no answers by RSA, for example ... . ) Mathematically the above statement is not the end of the story, because the security of encryption strongly depends on the possible set and probability distribution of programs we encrypt or the type of information we want to hide. Also, we cannot guarantee security if the program itself is badly designed. For example it prints itself out as first step - the movement of the head, and the read-write operations still can look as random. But there are not so trivial examples too. See Barak et al., who uses a stronger definition of obfuscation - a so called virtual black box property.

Because in real life we almost always know something about the program P, or cannot prove without further assumptions that it does not leak information as its feature, encrypting programs is a little bit of black art. So there is always a possibility of some hidden, so far not completely understood vulnerability. But this is also a case for text encryption. On the other hand, we can say as a general principle that it is always more secure to encrypt a program, than to run it in the celar.

For a less formal description see the previous section. For the most simple and important application see the third section.

The theoretical and practical consequences of this statement are enormous. It completely reshapes the vision about and understanding of computer, data and digital content security and integrity.  It has the potential to redefine and redistribute power, property and control in cyberspace.

But even if you do not trust our claim, you can think it as a mathematical conjecture. You can read these pages as an effort to uncover the technological, business and political consequences of the existence of such an algorithm. Anyway, so far no one has been able to disprove the possibility of its existence. You can suppose it. As people suppose most basic things in cryptography.

Back to Top

How the secure key hiding works?

By the help of the ideas mentioned above, we can eliminate the one of the most fundamental weaknesses of recently used software protection technologies. This weakness is as follows. By allowing or denying to run a particular program we always have a statement like this:

 if  the_key_is_correct  then  run_program

else  deny_access

This part of the program runs "in the clear" right before the eyes of hackers, pirates, ... . It is not encrypted. People try "to hide" it in various (clever and not so clever) ways in different parts of their programs, but computationally it is always relatively simple to find this crucial part. This is the main reason why software and other forms of digital piracy is so widespread and it has been so hopeless to fight against it without hardware solutions - at least so far. By using the previously described UPE technology, we can make a "holographic" version of the previous statement, mixing it non-locally with other parts of the program. By this extension, paying a small price in speed when starting the program, we can protect this routine and so the whole program - by using the standard and already "trusted" methods (which are usually broken in a few days, whatever the claims of their creators are). This technique is only an additional feature and certainly does not weaken other type of protection technology of the program.

Just to have an idea how surprising and counterintuitive is this little application of UPE, usually even top experts (like Bruce Schneier) - without precisely defining what they mean - reiterate conventional "wisdom", the so called Chess principle, which has never been proved mathematically, but quite the contrary, it turned out to be completely wrong.

By applying UPE we can prevent reverse engineering by making the executable so random - while computing the same function as the original program - that it will be incomprehensible under any circumstances. Unfortunately, it is a hard work to encrypt a program this way because we have to make it optimal for encryption. It is also decrease performance, which is sometimes not acceptable, even if only applied to a small part of the program. On the other hand, the good news is that by simple special hardware we can prevent this slowdown. TPVS develops this hardware.

By using the secure key hiding described above we can prevent illegal copying (in its most powerful form by a securely established server-client relationship). We can also control which programs we trust by checking signatures securely, which cannot be circumvented. This feature is fundamental in building first generation secure OS-es.

Back to Top

What are the closest mathematical results to UPE?

Secure mobile agents, secure mobile code, tamper resistant software, obfuscated code, computing by encrypted functions etc are other names of related research. A lot of partial results and interesting ideas but non of them is as general and powerful (both in security and performance) as UPE. All of them can be relatively easily cracked. Useful information and a lot of links can be found for example at Uni. Stuttgart or NIST. Almost non of the protocols are implemented. 

There is also an important paper of  Barak et al. - On the (im)possibility of obfuscating programs (extended abstract), Advances in Cryptology --- Crypto 2001 (Santa Barbara CA), pp. 1-18, Springer, Berlin, 2001. They propose a definition of obfuscator - satisfying a virtual black box property -, and show that there are some concrete algorithms, which cannot be obfuscated in this sense. They interpret their results that "there is no universal obfuscator". They also think, that their definition is very weak, although they are clearly see the necessity of exploring alternative definitions.

We use a  different, weaker, but somehow "implicite" definition for obfuscator. In this sense UPE is a universal one. (Barak et al. want to obfuscate certain programs which inner workings cannot be hidden, while UPE obfuscate "only" as much as possible, while giving back the best version of the code - from the point of view of security, while not guaranteeing any security. To establish the security of the encrypted program we have to prove it individually, using the security of UPE and the particular design of the program. The problem is that - without further studies of the particular program -  we can not know the security of the encrypted (obfuscated) program, because it may leak information in principle. The nice and important results of Barak et al. show that there is no royal road to code obfuscation, that every program and system is a different task if we want to encrypt (obfuscate) them.

This is a very important point. If there were universal obfuscators in the sense of Barak et al., the business and development model of TPVS should be different. We should concentrate on building the obfuscator, not caring much about the programs our users want to obfuscate. But their results show that this strategy does not work. We have to carefully study the programs in detail before obfuscating them. So the business and product development model of TPVS is not arbitrary, but comes from deep mathematics. Also, it shows why encrypted programs and systems are so rigid and difficult to make, even if we have much more flexibility than with traditional practices.

The little difficulty around the right definition of program encryption (obfuscation) shows the trickery of the field, which is only in embrionic phase. We have to be very careful with the (non-mathematical) language  we use. One always have to demand for the precise mathematical definitions. Unfortunately, in this field there are no crystallized concepts and every paper uses slightly different definitions, whose interpretation by ordinary words might cause serious confusion.

Back to Top

Are there other applications of UPE than security?

• We can reliably run an encrypted program on a physically unreliable hardware - decreasing hardware costs, or our software can work even under extreme circumstances. It will run, or crashes (so we can retry), but will not produce false results (only with extremely low probability). 
• We can check unreliable hardware (like FPGA)- before shipping, before a particular application or regularly as a maintenance. This way we can detact and prevent strange mistakes.
• During extremely big and long computations with a lot of self reference we can still ensure the reliability of our results.
  
• Maximally parallelizing computations (paradoxially speeding them up by slowing them down first).
• Real time computing - we can always predict the exact running time of the program.
• From an encrypted (that is completely homogenized) program we can make hardware almost trivially (compared to the difficulties of other type of  programs). This also explains, while it is so difficult to encrypt a program - practically we make a hardware first, which is usually very difficult.